number of available functions.
This page gives a brief overview of the functions in Calc-50.
For some more advanced examples of Calc-50 programming and graphics, see the
Calc-50 examples page.
News -- September 2020: Have some labels on the calculator keys become invisible?
That is caused by Apple's recent changes to iOS if your phone or iPad is in Dark Mode.
One fix is to go to to Settings / Display & Brightness and make sure Light Mode is on.
Calc-50 versions starting with 1.5 are ok in Dark mode.
The latest version on Apple's app store is version 1.6, October 2021.
Some minor improvements have been made to the plotting functions.
Version 1.5 was released in November 2020.
The main change from version 1.4 is to make the key labels stay visible when
the device is in Dark Mode.
New features for version 1.4 of June 2020:
Recent versions of the iPhone and iPad operating system cause apps to
start up more slowly, so a launch screen saying "Loading Calc-50"
might be visible briefly before the calculator screen appears.
New features for version 1.3 of March 2019:
There is a new key for extrapolation of sequences, series, and products. The
sum key can now automatically estimate infinite series, and the limit key
can handle more difficult limits.
New features for version 1.2 of July 2018:
User function definitions can now be longer, and programs that combine complex
arithmetic with real functions like sum and integrate are now easier to write.
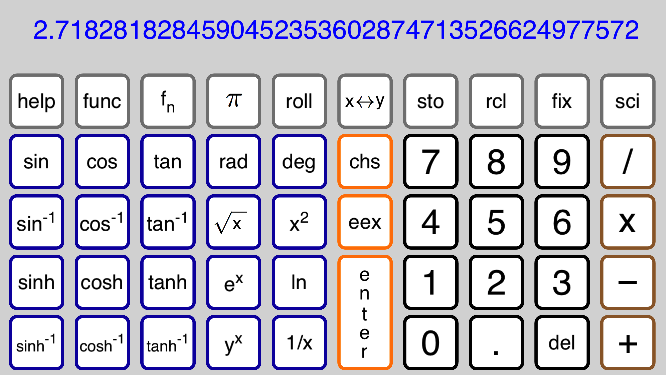
Calc-50 uses "RPN" input format, like classic scientific calculators such as the HP-15C.
This means the arguments are entered first, followed by the function.
For example, 2 + 3 is computed by pressing these keys: 2, enter, 3, +
These input values are kept in a 4-number stack. They are named x, y, z, t, where x is the
value displayed at the top of the screen. After 2, enter, 3 in the example above, y = 2 and
x = 3. Then the + operation adds x + y leaving 5 in x.
There are 101 storage registers, numbered 0 to 100, where values can be saved.
6, sto stores x in register 6, and 42, rcl recalls the value in register 42 and puts it into x.
Some fancier applications can use "index registers", as in 1, rcl, sto. This stores the
current x into whichever register is given by the value in register 1.
The fix key sets the number of digits after the decimal in the display. If x is 123.4567,
then 2, fix will display it as 123.46. The value of x is not changed, only the display
is different.
A negative number of digits signifies that large values are to be shown with commas.
-3, fix will show 12345.6789 as 12,345.679 in the display.
The sci key sets the number of significant digits to display in scientific notation.
If x is 123.4567, then 5, sci will display it as 1.2346e+2.
The display can show up to 50 digits. In fix mode, if x is too large or too
small for the
display, it will be shown in scientific mode.
Pressing the help key followed by another key brings up a screen like this one.

Each key on the calculator has an associated help screen with example usage, domain, and
sometimes a graph. Some general notes about Calc-50 can be found on the help screens for
digits 0, 1, 2, ....
The exit key then returns to the normal calculator screen.
The func key brings up one of 9 different sets of functions. The 20 keys in the lower left
change with each screen.
Pressing func by itself scrolls to the next screen, or pressing a digit from 1 to 9 followed
by func goes directly to that screen.
Screen 1 has the basic math functions: trig, exponentials, logs and powers.
Screen 2 has rounding to integers, max/min, random numbers, some statistical functions,
mod, power mod, gcd, and rational approximation:
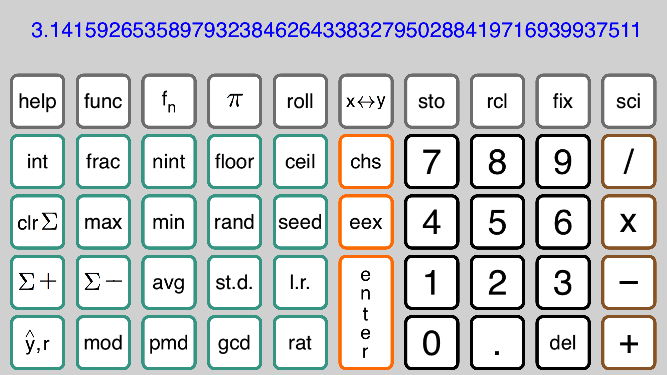
Screen 3 has factorial, gamma function, log gamma, combinations, permutations, the Euler
gamma constant, Bernoulli numbers, beta, psi, polygamma, pochhammer, error function,
incomplete gamma, incomplete beta. Also conversion between rectangular and polar form,
and absolute value.

Screen 4 has the exponential integral, sin, cos, sinh, cosh, and log integrals, Fresnel C and
S functions, Bessel J and Y functions.
Also time and calendar conversions, day of the week, percents,
hypotenuse, and last x.

Screen 5 has some financial functions that solve for various variables from a home
or auto loan.
After entering any 4 of the 5 values n (number of payments),
i (interest rate),
pv (present value), pmt (payment), fv (future value) using the store
keys, pressing the
remaining key computes that value.

Screen 6 has the keys used to define and edit user functions, and also 7 keys that use those
functions: derivative, nth derivative, maximum f(x), minimum f(x), integral of f(x) from
a to b, arc length of f(x) from a to b, solve f(x) = 0.
Depending on f(x), these functions can be slow. When a slow function is running, a
small spinning wheel is displayed above the help key and "running ..." appears in the
calculator output area to show that the function is still working.
The time key can be used to limit the running time for these functions.
Factoring integers with the fctr key is usually fast for integers up to about 30 or 40 digits.
Inputs up to 50 digits are allowed, and most of these can be factored, but some are slow.
The prog key allows for up to 10 user functions to be defined. Press a digit 0-9 followed
by prog to enter program mode and define a new function or edit an existing one.
For example, define function 6 to be cos( ci(x) ).
6, prog, clr f, 4, func, ci, 1, func, cos, 6, func, end
In program mode, before the end key is pressed, here is how the function definition looks:

The underscore _ after cos is the cursor. The 4 arrow keys move the cursor so a function
can be edited. The copy and paste keys let a function be copied and then pasted into another
function. The clrf key clears the function being edited, and bksp is a backspace that deletes
the operation immediately to the left of the cursor.
Pressing the end key puts the calculator back in normal mode. To evaluate function 6 at
x = 1.2 and compute cos( ci(1.2) ):
1.2, enter, 6, fn
With the calculator in radian mode, this function has a root near x = 0.117. To use the solve
key to find it, starting with 0.1 as an initial guess,
0.1, enter, 6, solv
The result is 0.117116.... Checking this by computing the function at this value (6, fn)
gives about -2.5e-57, indicating the root should be accurate to over 50 digits.
For another example, integrate this function from 1 to 3. To use the integrate key,
1, enter, 3, enter, 6, integrate
This numerical integration takes less than a second. The result is 1.86081....
Pressing x<->y to exchange the x and y registers shows y was about 1.0e-56, meaning
the integration algorithm stopped with the last two iterations agreeing to about 56 digits.
Screen 7 has more keys that involve user functions: graphics, limits, sums, extrapolation,
differential equations, and function selection.
The sum key can be used to do more than just simple sums. It can provide general loop
control for making lists and iterating recurrence relations.
For examples of this kind of programming, including some graphics applications, see the
Calc-50 examples page
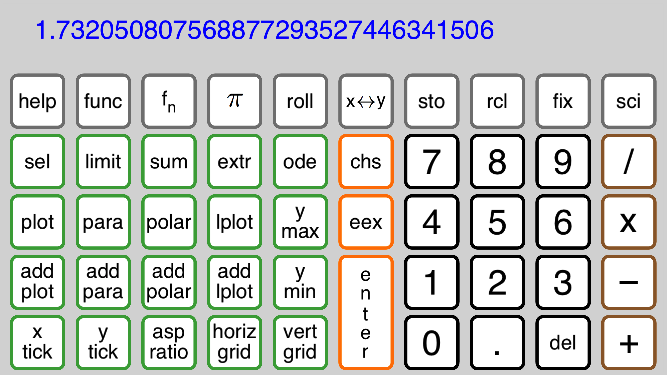
Four kinds of graphs are available: y = f(x) plots, parametric ( x(t), y(t) ) graphs,
polar r = f(theta) graphs, and list plots. Up to five graphs can be displayed at once
by using the add plot, ..., keys to add another graph to previously defined graphs.
Other keys can override the default settings for max and min y-values for the display
window, spacing for x and y axis tick marks, graph aspect ratio, horizontal and vertical
grid lines.
Use the plot key to graph f(x) = sin(3x) + cos(2x) from 0 to pi
7, prog, 1, sto, 3, *, 1, func, sin, 1, rcl, 2, *, cos, +, 6, func, end
7, func, 0, pi, 7, plot

Touching the screen in the graph area puts a small symbol on the screen at that location
and displays the (x,y) coordinates of that position at the bottom of the screen. Two buttons
appear next to the exit button, "zoom in" and "zoom out".

Zooming in re-draws the graph centered at the x-value shown at the bottom, with an
x-interval half as big as before. Zooming out does the same, with an x-interval twice
as big as before.
Screen 8 has unit conversion functions. Pressing a conversion key changes the value in the
x register from the units at the top of the key to the units at the bottom. Pressing the
inv key followed by a conversion key converts the other direction. The units of the result
are displayed along with its numerical value.

Screen 9 puts the calculator into complex arithmetic mode. The complex elementary
functions and basic arithmetic operations are provided.

To enter 1 + 2i, press
1, +i, 2, enter
Fewer digits can be displayed in complex mode for the real and imaginary parts of the
number, but each part still has over 50-digit accuracy internally.
The complex sto and rcl keys use 2 storage registers to hold one complex number.
5, sto while in complex mode will store the real part of x in register 5 and the imaginary
part in register 6. This can be used to communicate values between real and complex
modes, since registers 5 and 6 can be accessed separately from any real mode screen.
Why would anyone need 50-digit accuracy?
Most of the time, we don't. Most calculators have 14 to 16 digit accuracy, and exponent
ranges up to about 1.0e+1000. But some calculations need more accuracy or greater range.
Some of the most common applications for high-precision calculations involve deriving
formulas to be used in ordinary computer applications. If we want the coefficients in a
formula to be correctly rounded in the machine's double precision, then they usually must
be computed using higher precision.
An example of this is the derivation of the
Guass quadrature rule on the Calc-50 examples
page. If we used only double precision to do the derivation, the coefficients needed in the
formula would not be accurate to full precision.
Another feature of that derivation is that it uses binomial coefficients, derivatives, sums,
graphing, and equation solving in order to get the final formula. Most calculators do not
provide those operations.
Sometimes it can be hard to see that a formula is unstable and needs more accuracy, so it
is nice to have what seems like excessive precision available.
Here is a simple example. Examine the behavior of this function as x approaches zero.
f(x) = ( tan(sin(x)) - sin(tan(x)) ) / x^7
Doing f(0.03) on a standard calculator (TI-89) gives 0.033379, which is correct to only
3 significant digits.The older HP-15C calculator does even worse. It gives 0.0, no correct
digits at all.
The same calculation using Calc-50 gives .033367877648658374713095209129 when
displaying 30 digits. The formula is still losing accuracy, but by carrying 50 digits we can
afford to lose 11 digits in this unstable formula and still have plenty of accuracy left.
Getting closer to zero makes things even worse. The TI-89 gives f(0.001) = -100000.0
while Calc-50 shows .033333371693146997367349091810, still accurate to 30 places.
In 2020, the built-in calculator app for the iPhone does not have many mathematical
functions, but it does use its compiler's quadruple precision to provide about 34 digits.
It can get f(0.001) correct to 13 digits, but f(0.00001) has only 1 significant digit.
Calc-50 is starting to notice the instability for f(0.00001), getting "only" 27 digits correct.
For extreme cases like this, Calc-50 has one other trick for overcoming instability. The nth
derivative key on screen 6 works with derivative formulas that are also unstable, so it raises
precision above the user's 50-digit level to return accurate derivatives.
Defining f(x) as a user function on screen 6, the nth derivative key allows n = 0, meaning
it will evaluate our unstable function at higher precision. That gives f(0.00001) correct
to 50 digits.
Here is a second example. This time it is the exponent range that causes problems. Find
the probability of getting exactly one million heads if we toss a fair coin two million times.
This formula is
comb( 2e6 , 1e6 ) * (0.5)^2e6
where comb is the combination function, also called a binomial coefficient, and the second
term is 1/2 to the power two million.
The answer is about 0.000564, and this formula is not unstable. The problems for standard
calculators are that not all of them have a combination function, and the two numbers
comb( 2e6 , 1e6 ) = 5.5304e+602056 and (0.5)^2e6 = 1.0202e-602060
are far outside the exponent range of a normal calculator.
Summing up, some of the advantages Calc-50 over other calculators are:
- Many more functions available
- High precision means the user doesn't have to be as worried about moderately unstable
formulas losing too much precision
- Greater exponent range means fewer calculations fail because intermediate results
became too large or small
